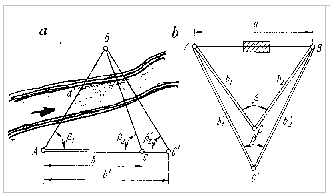
Jeigu reikia išmatuoti: atstumą, esant nepalankioms matavimui sąlygoms ir neturint tolimačio įgalinančio išmatuoti atstumą norimu tikslumu, ieškomasis atstumas: randamas netiesioginiu būdu iš vietovėje sudaryto trikampio. Pavyzdžiui, išmatuoti atstumą AB = d trukdo upė Sudarius vietovėje artimą lygiakraščiam trikampį, išmatuojame! atstumą AC = b, vadinamą baze ir teodolitu kampus β1 ir β2 tarp bazės ir kryties į taškai B. Ieškomas tos pačios linijos ilgis nustatomas sudarius kitą pagalbinį trikampį ABC. Atstumas šiuo atveju bus lygus: d1=bsinβ2/sin(β1+β2) Tikrinant tos pačios linijos ilgis nustatomas sudarius kitą pagalbinį trikampį ABC`. Atstumas šiuo atveju bus lygus: d1=b`sinβ`2/sin(β1+β`2) Jei skirtumas tarp d1 ir d2 neprašoka 1:500 nustatomo linijos ilgio, galutinis atstumas apskaičiuojamas kaip aritmetinis vidurkis, t.y. d1=d1+d2/2 Norint rasti atstumą tarp taškų A ir B kai tarp jų nėra matomumo topografinė nuotrauka, vietovėje reikia parinkti tašką C taip, kad būtų galima išmatuoti atstumus AC, BC ir kampą β. Skaičiuojant ieškomąjį atstumą, naudojamasi kosinusų formule d=saknis b12+b22 -2b1b2cosβ.
ŠIAIP ĮDOMUS VIDEO:
Komentarų nėra:
Rašyti komentarą